Reviewed:
On Growth and Form
Cambridge University Press, 345 pp., $31.00
Growing up the son of two scientists, in a house stuffed with thousands of books and journals, it was ironic that I discovered D’Arcy Wentworth Thompson’s On Growth and Form on the book stand at the corner Drug Fair store. I must have read half of it while hiding out behind the racks, which was no small feat — even the heavily abridged 1961 edition from Cambridge University Press runs to 345 dense pages. (The unabridged version of the Complete Revised Edition is an almost cubical 1,100 pages.) Long before finishing, I was pointedly reminded that the library was across the street. No matter; as it happened, we did have a copy at home. Of course we did. Our house had two subscriptions to The CDC’s Morbidity and Mortality Weekly Report: one for the adults, and one for the kids.
Completed in 1915 and first published in 1917, On Growth and Form had already been in print for 50 years when I found it, but it was revelatory: like opening the curtains and finding not the backyard but the Himalayas. Fourteen is an impressionable age, but any number of more mature readers have reacted in the same way, for Thompson’s book is not just about a theory of biology — it presents a way of seeing the natural world through ideas rendered as literature.
Too often, we’re introduced to the natural sciences by a route that seems designed to repel anyone with a degree of sensitivity to beauty: hacking away at brain-dead frogs, calculating the trajectory of imaginary cannon balls, and coaxing minuscule electric currents from vegetables. The scientific content of On Growth and Form has the opposite effect; it is about how a few simple mathematical principles dictate the structure of living things. Animals and plants are presented as the living embodiment of equations of scale across domains of linear measure, mass, temperature, speed; each plant and animal as a cloud of mathematical, almost Platonic, truths. Scientific principles are also revealed in the context of their connection to philosophy, history, and the elegant use of language and learning; a profound revelation of both the spaciousness and the interconnectedness of ideas. It is difficult to convey the impact this combination of ideas and writing delivers to a young mind at the right moment.
Peter Medawar famously called On Growth and Form “beyond comparison the finest work of literature in all the annals of science that have been recorded in the English tongue,” but it is not merely a literary expression of established knowledge; it’s one of the most peculiar and original works of modern science, advancing an idiosyncratic view of how organisms develop, a view that was deeply at odds with the intellectual climate of Thompson’s time. An elegant expression of an original idea that is still, possibly even increasingly, influential in biology, it’s a work of literature that can be read for pleasure by scientists and nonscientists, and a textbook on how to think in any field.
Stylistically, it has profoundly influenced generations of scientist-authors: Benoit Mandelbrot’s seminal The Fractal Geometry of Nature (1982) emulates both Thompson’s literary approach and his audacity in presenting a mathematical view of nature contrary to the prevailing view. Mandelbrot’s somewhat imperious style excites more admiration than affection. Oliver Sacks’ Migraine, which for many years was the most comprehensive overview of the field, though mostly nonmathematical, has more of Thompson’s grace and modesty. In this, Sacks may be Thompson’s truest heir. One of the lasting pleasures of On Growth and Form is in finding echoes of it in so many places, from the essays of Isaac Asimov, to Douglas Hofstadter’s Gödel , Escher, Bach, to Edward Tufte’s influential (and gorgeous) The Visual Display of Quantitative Information. One work contemporary with Thompson’s is also worth mentioning. The Curves of Life (1914) by Theodore Andrea Cook covers some of the same mathematical territory, particularly as related to natural spirals, but with a heavy emphasis on their occurrence in architecture and art.
*****
D’Arcy Thompson was born in Edinburgh in 1869, one year after the publication of Darwin’s The Origin of Species, and fifteen years before Einstein’s birth. Physics, in Thompson’s time, was a mature science, and highly mathematical — Boltzmann, Kelvin, Gibbs, Maxwell, and others had brought classical Newtonian physics to its apogee in the late 19th century; quantum mechanics and relativity, which burst on the scene just after the turn of the century, do not even have truly satisfying nonmathematical expressions. But in the first decades of the 20th century, biology still had one foot in the 19th; essentially premathematical, it was still as deeply connected to the spirit of natural philosophy as to modern science.
The epitome of the Victorian polymath, a classics scholar, mathematician, zoologist, and naturalist, Thompson is said to have been offered his choice of professorships in the Greek and Latin classics, mathematics, or zoology. He chose zoology, but his books are the products of a mind that integrates these disparate fields and more. Perhaps no other scholar could have written his Greek Birds and Greek Fishes, commentaries on every bird and fish mentioned in the extant classical Greek texts. One of the most famous and celebrated scientific personalities of the early 20th century, Thompson was also largely responsible for assembling the collection of the Bell Pettigrew Museum of Natural History at St. Andrews.
The first chapter of On Growth and Form is by far the most difficult for the typical modern reader. It is the only one that is not largely self-contained, and few modern readers without a background in philosophy and the history of science will be at home with the diversity of works and authors that are discussed or referred to (particularly Kant), and fewer still will be sufficiently at home with the languages a scholar educated in the late 19th century was expected to know: Greek, Latin, German, and French. For the rest of us, Google is invaluable. Entirely nonmathematical, chapter one lays out the philosophical background for the rest, primarily dealing with three themes: the shift away from the teleological orientation of premathematical scientific thought that accompanies maturation of a discipline into true science, the interdependence of philosophy and science, and the indispensability of mathematics to any scientific discipline.
Chapter two, my favorite, deals with simple mathematical principles that dictate how the form of an animal must change with size: why elephants cannot be shaped like deer; the nonintuitive relationship between leg size and walking speed (if mice moved at speeds proportional to their size, you wouldn’t need cats — you could just pick them up like box turtles); why birds can be only so large, and mammals only so small; why eyes vary in size so much less than animals do. Although Thompson died before computers were invented, this chapter made the analysis of algorithms — the study of how computational processes behave as problems increase in size — seem completely natural to me when I began to study computer science almost 70 years after the chapter was written.
While it’s not easy reading by any means, there are few ideas in the book that require mathematics beyond the level of advanced high school or the first year of college. (I was an undistinguished scholar in high school, to say the least, and got through it.) Given high school algebra and geometry, most of the concepts are developed from scratch, and are not difficult. If some of the technicalities do not get through, the strength of the writing usually bridges the gap, and getting every detail is not critical — they build to a fascinating and subtle argument that depends less on mastering the formulas themselves than understanding the general importance of their very existence.
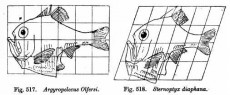
There are 17 chapters, covering an enormous range of issues, and not all have worn equally well scientifically, nor will all be of equal interest to the casual reader. But you can hardly crack the book without finding something fascinating: how the geometry that controls soap bubbles also determines a wide range of living forms; the geometrical order underlying the growth of shells, leaves, and horns; the engineering principles of skeletons. The most famous chapter is probably the last, which contains the best-known of the many illustrations in the book. The subject is the underlying unity of animal design — how a few basic designs can be systematically distorted to represent almost any animal by a process that we would now call morphing. The process is described by Thompson as simple manipulations of the grid on which they are drawn (in mathematical terms, replacing the regular X and Y coordinate values on the grid with smooth mathematical functions of these values). Less abstractly, it’s as if images that cannot be erased from or added to are drawn on a rubber sheet that can be stretched and compressed, but not cut. In this way, he warps a human infant’s skull into that of an ape, and turns one canonical fish into a multiplicity of species, showing how these simple warping functions unify huge families of species.
Darwin did not originate the idea that the species had evolved from ancient ancestors. His great discovery was natural selection, the mechanism by which evolution progresses, an insight that has had an impact on biology comparable to that of Newton’s laws of motion on physics. The discovery of the chemical mechanisms of inheritance was still two generations away in 1915, but the principles laid down by Darwin, and given structure by Mendel, were far along their way to becoming what they are today, the organizing principle of biology. Thus, it is striking how little mention of genetics there is in Thompson’s work, and here is a clue to something deeper.
The minimal reference to genetics in most of the book is not an accident or oversight. Thompson’s work ran profoundly against the grain of late 19th- and early 20th-century biology. He did not disbelieve in the principles of heredity (and said so), but he was at cross-purposes with most biologists in viewing genetic inheritance as not only having failed to yet explain some key aspects of the structure of animals, but as being inherently inadequate to ever explain them.
The Darwinian program had been (Thompson says), for 80 years, to link the species of life into a branching tree such that each species could be derived from another by incremental changes, all the way back to some origin. It was universally accepted that there must be gaps in the record, but there must be some way to see across the gaps, to infer a plausible path. Thompson believed the actual result was several distinct trees within which the model held nicely, but numerous gaps between the large categories that couldn’t be bridged by any plausible series of incremental changes.
The threefold thesis of On Growth and Form is ingenious, and easy to miss. Firstly, whatever the unknown mechanism of heredity might be, it seemed to operate at the level of the protein molecule, and at a larger scale, mathematically comprehensible physical forces, rather than molecules, appeared to dictate the forms of life. Secondly, within the large families of life, we could easily see how one species might be deformed into the other by incremental small changes (the Darwinian model), but gaps existed between the large families that couldn’t be bridged by incremental change. And finally, the gaps did not merely represent missing bits of history, or a failure of scientific imagination, because the families of mathematical functions that described these groupings also couldn’t be transformed into each other. In other words, there was something truly missing in the model that couldn’t simply be patched up.
The first 1,092 pages of the book are a series of almost independent essays illustrating the first point, and quietly laying the groundwork for the second two points, which the author makes explicit in the final two pages. It was a startling introduction of what would come, years later, to be called the “structuralist” view of biology, an approach that emphasizes the inter-connectedness of the whole organism and the difficulty of explaining all of evolution solely by a series of incremental genetic steps.
Structuralist biologists are not anti-Darwinian; to reject evolution by natural selection is to strictly exclude oneself from science — without it, we have only fairy tales — but they do emphasize that proteins and chemistry cannot be the whole story. The abridged Cambridge edition is one-third the weight of the complete Dover edition, making it more manageable on the train, but it is deeply flawed by the elision of the final five pages of the book, including the remarkable conclusion. The echoes of the social history of science and culture that can be inferred here are almost as intriguing as the key section left out.
Accepting the validity of evolution by natural selection separated the Yahoos from the Houyhnhnms as surely then as now. The editor’s original introduction carefully explained the basis of his decisions relating to what to leave out — some material was dropped because later research invalidated it, and other sections were simply too wordy or repetitive — but there is no acknowledgment of the removal of the conclusion, or even its existence. This remarkable editorial decision converted an argument of more than 1,100 pages into a collection of essays. This clearly exceeds any editor’s writ, the literary analog of the demolition of New York’s Pennsylvania Station two years later, and can only be interpreted as an attempt to bowdlerize away the radical content of the book, which in 1961 was nearly as controversial as it had been in 1917. Thankfully, the author’s brief epilogue was retained, despite opening with a single sentence referring to his startling conclusion: “The fact that I set little store by certain postulates (often deemed to be fundamental) of our present-day biology the reader will have discovered and I have not endeavored to conceal.” The rest is an exquisite example of a now-extinct variety of scholarly graciousness, which brings the book full circle, back to the subject of the first chapter, the place of mathematics, this time not in the sciences alone, but in literature, culture and the universe. It is worth the time to trace through the references, many unattributed or indirect, to Isaiah, Milton, Keats, Virgil, and others more obscure, in order to understand not just what the author is saying, but the author himself, and his beautiful lost world.
An addendum to the preface, by the same editor, added 30 years after the original, in 1991, refers extensively to the substance of the missing conclusion without actually mentioning its absence, perhaps by way of acknowledging the rising influence of the structuralist approach in the intervening decades. The loss of the critical pages is somewhat tempered by an excellent preface by Stephen Jay Gould (himself a noted structuralist biologist) that discusses the concluding argument, curiously, also without directly noting its absence from the text itself.
The First World War, which delayed the first publication of On Growth and Form for two years, closed an era of scholarship forever. The generation of scientists who followed Thompson were born into a world where steam power had still only begun to replace sail, but they came of age at the dawn of nuclear physics. The technology of modern warfare was only one aspect, perhaps not even the most destructive, of an exponential increase in learning across all fields that ended the heroic era of science. While there will probably never be a shortage of ideas in science, throughout the 20th century they increasingly occurred either at the finest grain or the farthest reaches; in either case, in the domain of the specialist, not the scholar or generalist. On Growth and Form may have been the last significant work of science in which a justification of the need for mathematics, or integration with the preceding century of philosophy, could be considered necessary, but this alone can’t account for its continuing popularity. Nor can the uniqueness of the ideas, as there is little in the book that is both still valid and not dealt with elsewhere in more modern form. A better explanation for its persistent popularity is its integration of culture and science — not just its language, but the way it exposes the roots of science in history, and embeds the discipline in the larger intellectual world.
Peter Coates is an artist, programmer, and writer living in Brooklyn.
Mentioned in this review:
On Growth and Form
The Fractal Geometry of Nature
Migraine
Gödel, Escher, Bach
The Visual Display of Quantitative Information
The Curves of Life
The Origin Of Species
